5.1 二叉树
本文最后更新于 2024-07-06,文章内容可能已经过时。
5.1 二叉树
一. 二叉树
1、定义
二叉树是另一种树形结构,其特点是每个结点至多只有两棵子树( 即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。
与树相似,二叉树也以递归的形式定义。二叉树是n (n≥0) 个结点的有限集合:
- 或者为空二叉树,即n=0。
- 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
二叉树是有序树,若将其左、右子树颠倒,则成为另一棵不同的二叉树。即使树中结点只有一棵子树,也要区分它是左子树还是右子树。二叉树的5种基本形态如图所示。

参考自:https://blog.csdn.net/Real_Fool_/article/details/113930623
2、特殊的二叉树
2.1、斜树
所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
2.2、满二叉树
满二叉树的叶子结点都集中在二叉树的最下一层,并且除叶子结点之外的每个结点度数均为2。
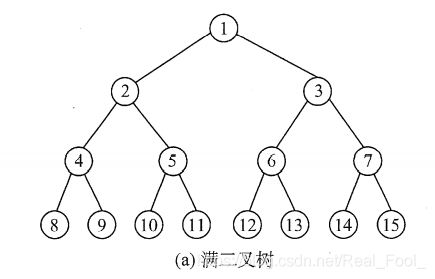
2.3、完全二叉树(Complete Binary Tree)
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
一棵二叉树至多只有最下面的一层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,而在最后一层上,右边的若干结点缺失的二叉树,则此二叉树成为完全二叉树。
特点:
- 叶子结点只可能在最大的两层上出现,对任意结点,若其右分支下的子孙最大层次为L,则其左分支下的子孙的最大层次必为L 或 L+1。
- 出于简便起见,完全二叉树通常采用数组而不是链表存储。
- 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
- 完全二叉树第i层至多有2i-1个节点,共i层的完全二叉树最多有2i-1个节点。
- 只允许最后一层有空缺结点且空缺在右边,即叶子结点只能在层次最大的两层上出现。
- 对任一结点,如果其右子树的深度为j,则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个。
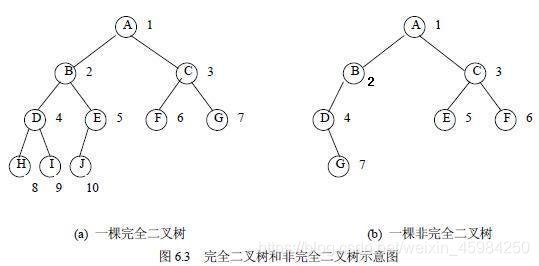
判断:完全二叉树:叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
参考自:https://blog.csdn.net/weixin_45984250/article/details/114932638
2.4、二叉排序树
左子树上所有结点的关键字均小于根结点的关键字;右子树上的所有结点的关键字均大于根结点的关键字;左子树和右子树又各是一棵二叉排序树。
2.5、平衡二叉树
二叉排序树的改进,树上任一结点的左子树和右子树的深度之差不超过1。
3、二叉树的存储结构
3.1、顺序存储结构
二叉树的顺序存储是指用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为i 的结点元素存储在一维数组下标为i − 1的分量中。
从数据存储来看,数组存储方式和树的存储方式可以相互转换,即数组可以转换成树,树也可以转换成数组。
对于一般的二叉树,为了让数组下标能反映二叉树中结点之间的逻辑关系,只能添加一些并不存在的空结点,让其每个结点与完全二叉树上的结点相对照,再存储到一维数组的相应分量中。
顺序存储二叉树的特点:
- 顺序二叉树通常只考虑完全二叉树
- 第n个元素的左子节点为 2 *n+ 1
- 第n个元素的右子节点为 2 *n+ 2
- 第n个元素的父节点为 (n-1) / 2
注:n 表示二叉树中的第几个元素(按0开始编号如图所示)
应用:堆排序。
3.2、链式存储结构
既然顺序存储适用性不强,我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。
三. 二叉树的遍历
- 先序遍历(PreOrder) :若二叉树不为空,则:访问根结点;先序遍历左子树;先序遍历右子树(根左右)。
- 中序遍历( InOrder):若二叉树不为空,则:先序遍历左子树;访问根结点;先序遍历右子树(左根右)。
- 后序遍历(PostOrder) :若二叉树不为空,则:先序遍历左子树;先序遍历右子树;访问根结点(左右根)。
四 . 二叉排序树
1、定义
二叉排序树(也称二叉查找树)或者是一棵空树,或者是具有下列特性的二叉树:
- 若左子树非空,则左子树上所有结点的值均小于根结点的值。
- 若右子树非空,则右子树上所有结点的值均大于根结点的值。
- 左、右子树也分别是一棵二叉排序树。
五.线索二叉树(Threaded Binary Tree)
n个结点的二叉树中含有n+1 【公式 2n-(n-1)=n+1】 个空指针域。利用二叉链表中的空指针域,存放指向该结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索”)。这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。一个结点的前一个结点,称为前驱结点;一个结点的后一个结点,称为后继结点。
六.代码实现
/**
* desc 二叉树的创建、查找和删除操作
* @author GreyPigeon mail:2371849349@qq.com
* @since 2024-01-23-15:52
**/
public class BinaryTreeDemo {
public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
//创建该二叉树方法:1.手动创建。2.通过递归的方式创建(以下为手动创建)
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//前序遍历查找
System.out.println("前序遍历查找~~~");
HeroNode resNode = binaryTree.preOrderSearch(5);
if (resNode != null) {
System.out.printf("找到了,信息为 no=%d name=%s\n", resNode.getNo(), resNode.getName());
} else {
System.out.printf("没有找到 no = %d 的英雄\n", 5);
}
//测试删除结点
System.out.println("删除前,前序遍历");
binaryTree.preOrder(); // 1,2,3,5,4
binaryTree.delNode(3);
System.out.println("删除后,前序遍历");
binaryTree.preOrder(); // 1,2,3,4
}
}
//定义BinaryTree 二叉树
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//删除结点
public void delNode(int no) {
if(root != null) {
//如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if(root.getNo() == no) {
root = null;
} else {
//递归删除
root.delNode(no);
}
}else{
System.out.println("空树,不能删除~");
}
}
//前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//中序遍历
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//前序遍历查找
public HeroNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//中序遍历查找
public HeroNode infixOrderSearch(int no) {
if(root != null) {
return root.infixOrderSearch(no);
}else {
return null;
}
}
//后序遍历查找
public HeroNode postOrderSearch(int no) {
if(root != null) {
return this.root.postOrderSearch(no);
}else {
return null;
}
}
}
//创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; //默认null
private HeroNode right; //默认null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
/**递归删除结点
1.如果删除的节点是叶子节点,则删除该节点
2.如果删除的节点是非叶子节点,则规则如下:
如果该非叶子节点A只有一个子节点B,则子节点B替代节点A;
如果该非叶子节点A有左子节点B和右子节点C,则让左子节点B替代节点A。
*/
public void delNode(int no) {
//2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if(this.left != null && this.left.no == no) {
if (this.left.left != null && this.left.right != null) {
HeroNode them = this.left.right;
this.left = this.left.left;
this.left.right = them;
return;
}
if (this.left.left == null && this.left.right != null) {
this.left = this.left.right;
return;
}
if (this.left.left != null && this.left.right == null) {
this.left = this.left.left;
}
return;
}
//3.如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if(this.right != null && this.right.no == no) {
if (this.right.left != null && this.right.right != null) {
HeroNode them = this.right.right;
this.right = this.right.left;
this.right.right = them;
return;
}
if (this.right.left == null && this.right.right != null) {
this.right = this.right.right;
return;
}
if (this.right.left != null && this.right.right == null) {
this.right = this.right.left;
}
return;
}
//4.我们就需要向左子树进行递归删除
if(this.left != null) {
this.left.delNode(no);
}
//5.则应当向右子树进行递归删除
if(this.right != null) {
this.right.delNode(no);
}
}
//前序遍历
public void preOrder() {
System.out.println(this);
//递归向左子树前序遍历
if(this.left != null) {
this.left.preOrder();
}
//递归向右子树前序遍历
if(this.right != null) {
this.right.preOrder();
}
}
//中序遍历
public void infixOrder() {
//递归向左子树中序遍历
if(this.left != null) {
this.left.infixOrder();
}
//输出父结点
System.out.println(this);
//递归向右子树中序遍历
if(this.right != null) {
this.right.infixOrder();
}
}
//后序遍历
public void postOrder() {
if(this.left != null) {
this.left.postOrder();
}
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
/**
* 前序遍历查找
* @param no 查找no
* @return 如果找到就返回该Node ,如果没有找到返回 null
*/
public HeroNode preOrderSearch(int no) {
//比较当前结点是否相等
if(this.no == no) {
return this;
}
//1.则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
//2.如果左递归前序查找,找到结点,则返回
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {//说明我们左子树找到
return resNode;
}
//1.左递归前序查找,找到结点,则返回,否继续判断,
//2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序遍历查找
public HeroNode infixOrderSearch(int no) {
//判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入中序查找");
//如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点
if(this.no == no) {
return this;
}
//否则继续进行右递归的中序查找
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//后序遍历查找
public HeroNode postOrderSearch(int no) {
//判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {//说明在左子树找到
return resNode;
}
//如果左子树没有找到,则向右子树递归进行后序遍历查找
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入后序查找");
//如果左右子树都没有找到,就比较当前结点是不是
if(this.no == no) {
return this;
}
return resNode;
}
}
```java
/**
* desc 实现顺序存储二叉树(以前序遍历为例)
* @author GreyPigeon mail:2371849349@qq.com
* @since 2024-01-24-20:48
**/
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
//创建一个 ArrBinaryTree
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
arrBinaryTree.preOrder(); // 1,2,4,5,3,6,7
}
}
//编写一个ArrayBinaryTree, 实现顺序存储二叉树遍历
class ArrBinaryTree {
private int[] arr;//存储数据结点的数组
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
//重载preOrder
public void preOrder() {
this.preOrder(0);
}
/**
* 编写一个方法,完成顺序存储二叉树的前序遍历
* @param index 数组的下标
*/
public void preOrder(int index) {
//如果数组为空,或者 arr.length = 0
if(arr == null || arr.length == 0) {
System.out.println("数组为空,不能按照二叉树的前序遍历");
}
//输出当前这个元素
System.out.print(arr[index] + " ");
//向左递归遍历
if((index * 2 + 1) < arr.length) {
preOrder(2 * index + 1 );
}
//向右递归遍历
if((index * 2 + 2) < arr.length) {
preOrder(2 * index + 2);
}
}
}
```java
/**
* desc 线索二叉树的实现和遍历
* @author GreyPigeon mail:2371849349@qq.com
* @since 2024-01-26-20:46
**/
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
//测试一把中序线索二叉树的功能
HeroNode root = new HeroNode(1, "tom");
HeroNode node2 = new HeroNode(3, "jack");
HeroNode node3 = new HeroNode(6, "smith");
HeroNode node4 = new HeroNode(8, "mary");
HeroNode node5 = new HeroNode(10, "king");
HeroNode node6 = new HeroNode(14, "dim");
//二叉树,后面我们要递归创建, 现在简单处理使用手动创建
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
//测试中序线索化
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
threadedBinaryTree.threadedNodes();
//测试: 以10号节点测试
HeroNode leftNode = node5.getLeft();
HeroNode rightNode = node5.getRight();
System.out.println("10号结点的前驱结点是 =" + leftNode); //3
System.out.println("10号结点的后继结点是=" + rightNode); //1
//当线索化二叉树后,能在使用原来的遍历方法
//threadedBinaryTree.infixOrder();
System.out.println("使用线索化的方式遍历 线索化二叉树");
threadedBinaryTree.threadedList(); // 8, 3, 10, 1, 14, 6
}
}
//定义ThreadedBinaryTree 实现了线索化功能的二叉树
class ThreadedBinaryTree {
private HeroNode root;
//为了实现线索化,需要创建要给指向当前结点的前驱结点的指针
//在递归进行线索化时,pre 总是保留前一个结点
private HeroNode pre = null;
public void setRoot(HeroNode root) {
this.root = root;
}
//重载一把threadedNodes方法
public void threadedNodes() {
this.threadedNodes(root);
}
//遍历线索化二叉树的方法
public void threadedList() {
//定义一个变量,存储当前遍历的结点,从root开始
HeroNode node = root;
while(node != null) {
//循环的找到leftType == 1的结点,第一个找到就是8结点
//后面随着遍历而变化,因为当leftType==1时,说明该结点是按照线索化
//处理后的有效结点
while(node.getLeftType() == 0) {
node = node.getLeft();
}
//打印当前这个结点
System.out.println(node);
//如果当前结点的右指针指向的是后继结点,就一直输出
while(node.getRightType() == 1) {
//获取到当前结点的后继结点
node = node.getRight();
System.out.println(node);
}
//替换这个遍历的结点
node = node.getRight();
}
}
/**
* 编写对二叉树进行中序线索化的方法
* @param node 就是当前需要线索化的结点
*/
public void threadedNodes(HeroNode node) {
//如果node==null, 不能线索化
if(node == null) {
return;
}
//(一)先线索化左子树
threadedNodes(node.getLeft());
//(二)线索化当前结点[有难度]
//处理当前结点的前驱结点
if(node.getLeft() == null) {
//让当前结点的左指针指向前驱结点
node.setLeft(pre);
//修改当前结点的左指针的类型,指向前驱结点
node.setLeftType(1);
}
//处理后继结点
if (pre != null && pre.getRight() == null) {
//让前驱结点的右指针指向当前结点
pre.setRight(node);
//修改前驱结点的右指针类型
pre.setRightType(1);
}
//!!! 每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = node;
//(三)在线索化右子树
threadedNodes(node.getRight());
}
}
//先创建HeroNode 结点
class HeroNode {
private int no;
private String name;
private HeroNode left; //默认null
private HeroNode right; //默认null
//说明
//1. 如果leftType == 0 表示指向的是左子树, 如果 1 则表示指向前驱结点
//2. 如果rightType == 0 表示指向是右子树, 如果 1表示指向后继结点
private int leftType;
private int rightType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
}
- 感谢你赐予我前进的力量



