5.0 树（Tree）

一. 定义

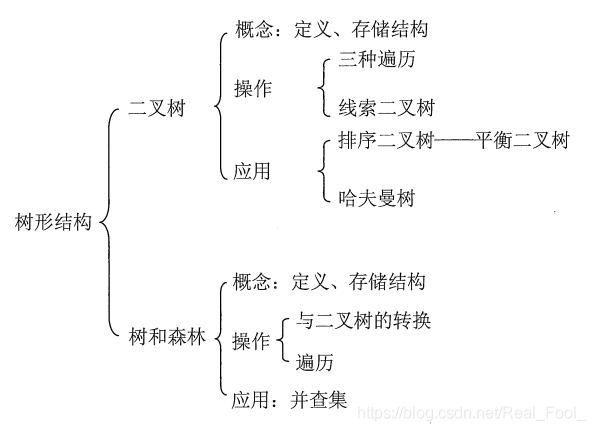
树是n（n>=0）个结点的有限集。当n = 0时，称为空树。在任意一棵非空树中应满足：

• 有且仅有一个特定的称为根的结点。
• 当n>1时，其余节点可分为m（m>0）个互不相交的有限集T1,T2,…,Tm，其中每个集合本身又是一棵树，并且称为根的子树。

显然，树的定义是归的，即在树的定义中又用到了自身，树是一种递归的数据结构。树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点：

• 树的根结点没有前驱，除根结点外的所有结点有且只有一个前驱。
• 树中所有结点可以有零个或多个后继。

因此n个结点的树中有n-1条边。

结点K的祖先：根A到结点K的唯一路径上的任意结点。

K的双亲：路径上最接近结点K的结点E称为K的双亲,而K为结点E的孩子。根结点A是树中唯一没有双亲的结点。

兄弟结点：有相同双亲的结点称为兄弟,如结点K和结点L有相同的双亲E,即K和L为兄弟。
结点的度：树中一个结点的孩子个数。树中结点的最大度数称为树的度。如结点B的度为2,结点D的度为3,树的度为3。
分支结点(又称非终端结点)：度大于0的结点。

叶子结点(又称终端结点)：度为0(没有子女结点)的结点。在分支结点中,每个结点的分支数就是该结点的度。
结点的层次：从树根开始定义,根结点为第1层,它的子结点为第2层,以此类推。双亲在同一层的结点互为堂兄弟。
结点的深度：是从根结点开始自顶向下逐层累加的。
结点的高度：是从叶结点开始自底向上逐层累加的。
树的高度(或深度)：是树中结点的最大层数。
有序树和无序树：树中结点的各子树从左到右是有次序的,不能互换,称该树为有序树,否则称为无序树。
路径和路径长度：树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
注意:由于树中的分支是有向的,即从双亲指向孩子,所以树中的路径是从上向下的,同一双亲的两个孩子之间不存在路径。
森林：m (m≥0)棵互不相交的树的集合。(只要把树的根结点删去就成了森林)

参考自：https://blog.csdn.net/Real_Fool_/article/details/113930623